INTRODUCTION OF Geometric Foundations of Motion and Control

INTRODUCTION

We describe below a geometric framework that leads to a better understanding of locomotion generation and motion control in mechanical systems. This introduction provides some basic examples that motivate and set the stage for this framework.

Perhaps the most popular example of the generation of rotational motion is the failing cat, which is able to execute a 180º reorientation, all the while having zero angular momentum. It achieves this by manipulating its joints to create shape changes. To understand this, one has to remember that the angular momentum of a rotating rigid object is its moment of inertia times its instantaneous angular velocity; this is the angular version of the familiar relation ''momentum equals mass times velocity.'' Shape changes result in a change in the cat's moment of inertia and this, together with the constancy of the angular momentum, creates the overall orientation change. However, the exact process by which this occurs is subtle, and intuitive reasoning can lead one astray. While this problem has been long studied (e.g., by Kane and Shur, 1969), recently new and interesting insights have been discovered using geometric methods (see Enos, 1993; Montgomery, 1990, and references therein).

Astronauts who wish to reorient themselves in a free space environment can similarly do so by means of shape changes. For example, holding one of their legs straight, they can swivel it at the hip, moving their foot in a circle. When they have achieved the desired orientation, they merely stop their leg movement. Similar movements for robots and spacecraft can be controlled automatically to achieve desired objectives (see, for example, Walsh and Sastry, 1995). One often refers to the extra motion that is achieved as thegeometric phase.

The history of this phenomenon and its applications is a long and complex story. We shall only mention a few highlights. Certainly the shift in the plane of the swing in the Foucault pendulum as the earth rotates once around its axis is one of the earliest examples of this phenomenon. Anomalous spectral shifts in rotating molecules are another. Phase formulas for special problems such as rigid body motion and polarized light in helical fibers were understood already in the early 1950s. Additional historical comments and references can be found in Berry (1990), and Marsden and Ratiu (1994). Gradually the subject became better understood, but the first paper to clarify and emphasize the ubiquity of the geometry behind all these phenomena was Berry (1985). It was also quickly realized that the phenomenon occurs in essentially the same way in both classical and quantum mechanics (Hannay, 1985), and that the phenomenon can be linked in a fundamental way with the presence of symmetry (Montgomery, 1988; Marsden et al., 1990).

The theory of geometric phases has an interesting link with noneuclidean geometry, a subject first invented for its own sake, without regard to applications. A simple way to explain this link is as follows. Hold your hand at arm's length, but allow rotation in your shoulder joint. Move your hand along three great circles, forming a triangle on the sphere, and during the motion, keep your thumb "parallel," that is, forming a fixed angle with the direction of motion. After completing the circuit around the triangle, your thumb will return rotated through an angle relative to its starting position (see Figure 1.1). In fact, this angle (in radians) is given by Θ = Δ-π where Δ is the sum of the angles of the triangle. The fact that  is of course one of the basic facts of noneuclidean geometry—in curved spaces, the sum of the angles of a triangle is not necessarily z (i.e., 180º). This angle is also related to the area A enclosed by the triangle through the relation Θ = A/r², where r is the radius of the sphere.

The examples presented so far are rather different from what one finds in many other mechanical systems of interest in one crucial aspect—the absence of constraints of rolling, sliding, or contact. For example, when one parks a car, the steering mechanism is manipulated and movement into the parking spot is generated; obviously the rolling of the wheels on the road is crucial to the maneuver. When a human or a robot manipulates an object in its fingers (imagine twirling an egg in your fingers), it can reorient the object through the rolling of its fingers on the object. This can be shown in a demonstration I learned from Roger Brockett: roll your fingers in a rotating motion on a ball resting on a table—you will find that the ball reorients itself under your finger! The amount of rotation is again related to the amount of area you capture in the rotating motion. You have generated rotational motion! (See Figure 1.2.)

Suggested Citation:"1: GEOMETRIC FOUNDATIONS OF MOTION AND CONTROL." National Research Council. 1997. Motion, Control, and Geometry: Proceedings of a Symposium. Washington, DC: The National Academies Press. doi: 10.17226/5772.

×

Save

Cancel

FIGURE 1.1 A parallel movement of your thumb around a spherical triangle produces a phase shift.

FIGURE 1.2 Rolling your finger in a circular motion on a rolling sphere generates rotations.

Suggested Citation:"1: GEOMETRIC FOUNDATIONS OF MOTION AND CONTROL." National Research Council. 1997. Motion, Control, and Geometry: Proceedings of a Symposium. Washington, DC: The National Academies Press. doi: 10.17226/5772.

×

Save

Cancel

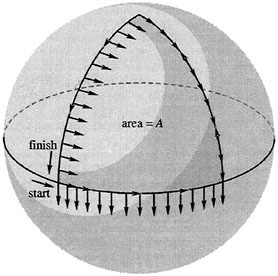
In all these cases, cyclic motion in one set of variables (often called theinternal variables) produces motion in another set (often called the groupvariables). This idea is central to the basic geometric framework described in ensuing sections.

One can generate translational motion as well as rotational motion. For example, microorganisms and snakes generate translations by a very specific cyclic manipulation of their internal variables (Shapere and Wilczek, 1987). The reason for this is, in a superficial sense, that in these examples, translation is kinematically possible (translations are available as group variables) and the controls are such that these variables are activated. Often translational motion and rotational motion are coupled in interesting ways, as in the snakeboard, a modification of the familiar skateboard. This modification allows the rider to rotate the front and back wheels by rotating his feet and this, together with the rotary motion of the rider's body, allowsboth translational and rotational motion to be generated. Such motion can be controlled with the objective that desired motions be generated. We will discuss this example in a little more detail in the section entitled "The Snakeboard," below.

The generation of motion in small robotic devices is very promising for medical applications. In this context, one seeks devices that can move in confined spaces under variable conditions (flexible walls, tight comers, etc.). In fact, this general philosophy is one of the reasons one hopes that medical operations in the future will be much less intrusive than many of them are now.

There are similar links between vibratory motion and translational and rotational motion (e.g., the developments of micromotors) (Brockett, 1989), on the one hand, and, on the other hand, motion generation in animals (e.g., the generation and control of waves from coupled oscillators, as seen in the swimming of fish and in the locomotion of insects and other creatures).

A central question to address in this area is, How should one control motions of the internal variables so that the desired group (usually translational and rotational) motions are produced? To make progress on this question, one needs to combine experience with simple systems and strategies—such as steering with sinusoids, as in Murray and Sastry (1993)—with a full understanding of the mathematical structure of the mechanical systems, both analytical and geometrical. We also mention the work of Brockett (1981), which shows that for certain classes of control systems that are controllable via first level brackets, steering by sinusoids is, in fact, optimal.