The snakeboard is an interesting example that illustrates several of the ideas we have been discussing (see Lewis et al., 1997). This device is a modification of the standard skateboard, the most important of which is that riders can use their feet to independently turn the front and back wheels—in the standard skateboard, these wheels are of course fixed to the frame of the skateboard. In addition, one can manipulate one's body using a swivelling motion and this motion is coupled to the motion of the snakeboard itself. We show the snakeboard schematically in Figure 1.7.
One of the fascinating things about the snakeboard is that one can generate locomotion without pedaling, solely by means of internal motions. When the user's feet and body are moved in the right way, rotational and translational motion of the device can be generated. The snakeboard is simple enough that one can study many parts of it analytically and numerical simulations of its motion are reasonably economical to implement. On the other hand, it seems to have all of the essential features that one would want for more complex systems, the main one for the present goals being its ability to generate rotational and translational motion. From the mathematical and mechanical point of view, it is rich in geometry and in symmetry structure, which also makes it attractive. Thus, it provides a good testing and development ground for both theoretical and numerical investigations.
From the theoretical point of view, one feature of the snakeboard that sets it truly apart from examples like the planar skater and the falling cat is that even though it has the symmetry group of rotations and translations of the plane, the linear and angular momentum is not conserved. Recall that for the planar skater, no matter what motions the arms of the device make, the values of the linear and angular momentum cannot be altered. This is not true for the snakeboard and this can be traced to the presence of the forces of constraint, just as in the rattleback mentioned earlier. Thus, one might suspect that one should abandon the ideas of linear and angular momentum for the snakeboard.
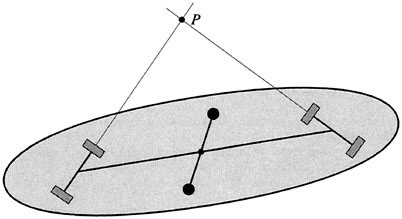
However, a deeper inspection shows that this is not the case. In fact, one finds that there is a special component of the angular momentum, namely that about the point P shown in Figure 1.8.
If we call this component p, one finds that, due to the translational and rotational invariance of the whole system, there is a ''momentum equation'' for p of the form
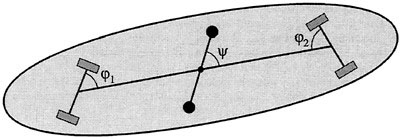
FIGURE 1.7 The snakeboard has three movable internal parts, the front and back wheels and the angle of the rider's body.
where x represents the internal variables of the system (the three angles shown in the preceding figure). The point is that this equation does not depend on the rotational and translational position of the system. Thus, if one has a given internal motion, this equation can be solved for p and, from it, the attitude and position of the snakeboard calculated by means of another integration. This strategy is thus parallel to that for the falling cat and the planar skater.
With this set-up, one is now in a good position to identify the resulting geometric phase with the holonomy of a connection that is a synthesis of the kinematic and mechanical connection. Carrying this out and implementing these ideas for more complex systems is in fact the subject of current research.







No comments:
Post a Comment