CONNECTIONS AND BUNDLES

One of the fruitful ideas from geometry that has been used in the investigation of mechanical systems is that of a connection. While the notion of a connection is quite precise, connections have many personalities. On the one hand, one thinks of them as describing how curved a space is; in fact, in the classical Riemannian setting used by Einstein in his theory of general relativity, the curvature of the space is constructed out of the connection (in that case, also called the Christoffel symbols). In other, but related, settings developed by Eli Cartan, the connection is what is responsible for a corrected measure of acceleration; for example, if one is on a rotating merry-go-round, one has to correct any measurement of acceleration to take into account the acceleration of the merry-go-round, and this correction can be described by a connection.

In the general theory, connections are associated with mappings, calledbundle mappings, that project larger spaces onto smaller ones, as in Figure 1.3. The larger space is called the bundle and the smaller space is called the base. Directions in the larger space that project to zero are called vertical directions. The general definition of a connection is a specification of a set of directions, called horizontal directions, that complements at each point the space of vertical directions.

In the example of parallel transport of the thumb around the sphere, the larger space is the space of all tangent vectors to the sphere, and this space projects to the sphere itself by projecting a vector to its point of attachment to the sphere. The horizontal directions are the directions with zero acceleration within the intrinsic geometry of the sphere; that is, the directions determined by great circles.

In the thumb example, we saw that going around the triangle produces a change in the orientation of the thumb on return. The thumb is parallel transported, that is, it moves in horizontal directions with respect to the connection. The thumb has undergone a rotational shift from the beginning to the end of its journey.

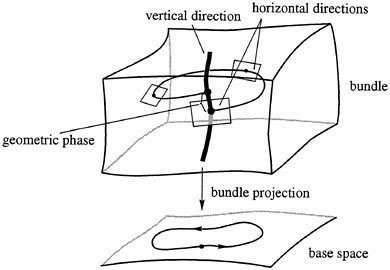
Figure 1.3 A connection divides the space into vertical and horizontal directions.

In general, we can expect that if we have a horizontal motion in the bundle and if the corresponding motion in the base is cyclic, then the horizontal motion will undergo a shift, which we will call a phase shift, between the beginning and the end of its path. The shift in the vertical direction is often given by an element of a group, such as a rotation or translation group. In many of the examples discussed so far, the base space is the control space in the sense that the path in the base can be chosen by suitable controls. The path above it in the bundle is regarded as being determined by the condition of horizontality. This condition therefore determines its phase.

This setting of connections provides a framework in which one can understand the phrase we started with: when one variable in a system moves in a periodic fashion, motion of the whole object can result. Here, the "motion of the whole object" is represented by the geometric phase. Coming along with this notion are plenty of lovely theorems and calculational tools; for example, one of these (based on Stokes' theorem) shows how to calculate the geometric phase in terms of the integral of the curvature of the connection over an area enclosed by the closed curve on the base. This is one reason that areas so commonly appear in geometric phase formulas.

Connections are ubiquitous in geometry and physics. For example, connections are one of the main ingredients in the modem theory of elementary particles, and are the primary fields in Yang-Mills theory, a generalization of Maxwell's electromagnetic theory. In fact, in electromagnetism, the equation 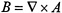 for the magnetic field may be thought of as an expression for the curvature of the connection (or magnetic potential) A.