CONSTRAINTS: ANGULAR MOMENTUM AND ROLLING

In many mechanical systems, there are conditions called "constraints." For our purposes, these are of two fundamentally different sorts. The first is typified by the constraint of zero angular momentum for the falling cat. The cat, once released, and before it reaches the ground, cannot change the fact that its angular momentum is zero, no matter how it moves its body parts. We choose the cat's base space to be its shape space, which does indeed literally mean what it says—the collection of all the shapes of its body, which can be specified by giving the angles between its body parts. The bundle in this case consists of these shapes together with a rotation and translation to specify the position and orientation in space. Since the cat is free to manipulate its shape using its muscles, it can perform maneuvers, some of them cyclic, in shape space. Meanwhile, how the cat turns in space is governed by the law of conservation of angular momentum. It turns out that this law exactly defines the horizontal space of a connection! The connection in this case is called the "mechanical connection." That this corresponds to a connection was discovered through the combined efforts of Smale (1970), Abraham and Marsden (1978), and Kummer (1981). Thus, when one puts together the theory of connections with this observation, and throws in control theory, one has the beginnings of the "gauge theory of mechanics." This theory has been extended and developed by many workers since then.

Observation of the motions of a mechanical system in its shape space shows a relation to the theory of reduction, a theory that seeks to make the configuration space of a mechanical system smaller by taking advantage of symmetries. This method has led to many interesting and unexpected discoveries about mechanics, including, for example, the explanation of the integrability of the Kowaleskaya top in terms of symmetry by Bobenko et al. (1989). (An algebraic-geometric construction with similar goals was found by Haine, Horozov, Adler, and van Moerbeke around the same time.) Observing the motion in shape space alone is similar to watching the shapes change relative to an observer riding with the object. In such a frame, one sees what seem to be extra forces, namely the Coriolis and centrifugal forces. In fact, these forces can be understood in terms of the curvature of the mechanical connection. Then the problem of finding the original complete path is one of finding a horizontal path above the given one. This is sometimes called the "reconstruction problem." We conclude that the generation of geometric phases is closely linked with the reconstruction problem.

One of the simplest systems in which one can see these phenomena is called the planar skater. This device consists of three coupled rigid bodies lying in the plane. They are free to rotate and translate in the plane, somewhat like three linked ice hockey pucks. This has been a useful model example for a number of investigations, and was studied fairly extensively in Oh et al. (1989), and Krishnaprasad (1989) and references therein. The only forces acting on the three bodies are the forces they exert on each other as they move. Because of their translational and rotational invariance, the total linear and angular momentum remains constant as the bodies move. This holds true even if one applies controls to the joints of the device; this is because the conservation of momentum depends only on externally applied forces and torques. See Figure 1.4.

The planar skater illustrates well some of the basic ideas of geometric phases. If the device starts with zero angular momentum and it moves its arms in a periodic fashion, then the whole assemblage can rotate, keeping, of course, zero angular momentum. This is analogous to our astronaut in free space who rotates his arms or legs in a coordinated fashion and finds that he rotates. One can understand this simple example directly by using conservation of angular momentum. In fact, the definition of angular momentum allows one to reconstruct the overall attitude of the device in terms of the motion of the joints using freshman calculus. Doing so, one gets a motion generated in the overall attitude, which is indeed a geometric phase. This example is sufficiently simple that one does not need the geometry of connections to understand it, but nonetheless it provides a simple situation in which one can test the ideas. For more complex examples, such as the falling cat, the geometric setting of connections has indeed proven useful.

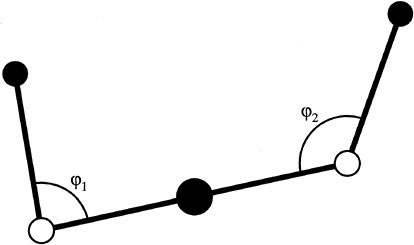
FIGURE 1.4 The planar skater consists of three interconnected bodies that are free to rotate about their joints.

To indicate some of the flavor of three-dimensional examples, we discuss the rigid body. Each position of the rigid body is specified by a Euclidean motion giving the location and orientation of the body. The motion is then governed by the equations of mechanics in this space. Assuming that no external forces act on the body, conservation of linear momentum allows us to solve for the components of the position and momentum vectors of the center of mass. Passage to the center of mass frame reduces one to the case where the center of mass is fixed, so only pure rotations remain. Each possible orientation corresponds to the specification of a proper orthogonal matrix A. Back in 1740, Euler parametrized the

matrix A in terms of three (Euler) angles between axes that are either fixed in space or are attached to symmetry planes of the body's motion.

We regard the element 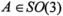 giving the configuration of the body as a mapping of a reference configuration to the current configuration. The matrix A takes a reference or label point X to a current point x = A(X). For a rigid body in motion, the matrix A is time dependent and the velocity of a point of the body is 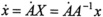. Since A is an orthogonal matrix, we can write 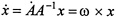, which defines the spatial angular velocity vector ω .The corresponding body angular velocity is defined by Ω; = A^-1ω, so that Ω; is the angular velocity as seen in a body-fixed frame. The kinetic energy is given by integrating the kinetic energy expression for particles (one-half the mass density times the square of the velocity) over the reference configuration. In fact, this kinetic energy is a quadratic function of Ω;. Writing  defines the (time independent) moment of inertia tensor I, which, if the body does not degenerate to a line, is a positive definite 3 × 3 matrix, or better, a quadratic form. Every calculus student learns how to calculate moments of inertia as illustrations of the process of multiple integration.

The equations of motion in A space define certain equations in Ω; space that were discovered by Euler: 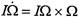. The body angular momentum is defined, analogous to linear momentum p = mv, as Π = IΩ;. In terms of Π, the Euler equations read Π = Π × Ω;. This equation implies that the spatial angular momentum vector π = AΠ is fixed in time. One may view this fact as a conservation law that results from the rotational symmetry of the problem. These and other facts given here are proven in every mechanics textbook, such as Marsden and Ratiu (1994).

Viewing the components (Π₁,Π₂,Π₃) of Π as coordinates in three-dimensional space, the Euler equations are evolution equations for a point in this space. A constant of motion for the system is given by the square length of the total angular momentum vector: 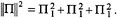. This follows from conservation of π and the fact that  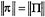or can be verified directly from the Euler equations by computing the time derivative of .

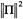Because of conservation of 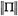, the evolution in time of any initial point Π(0) is constrained to the sphere 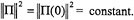. Thus we may view the Euler equations as describing a two-dimensional dynamical system on an invariant sphere. This sphere is called the reduced-phase space for the rigid body equations. Another constant of the motion is the Hamiltonian or energy: 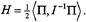. Since solutions curves are confined to the sets where H is constant, which are in general ellipsoids, as well as to the invariant spheres where  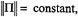= constant, the intersection of these surfaces is precisely that of the trajectories of the rigid body, as shown in Figure 1.5.

Let us briefly indicate how geometric phases come into the rigid body example. Suppose we are given a trajectory Π(t) on P_μ that has period T and energy E. After time T the rigid body has rotated in physical 3-space about the axis μ by an angle given by

Here Λ is the solid angle enclosed by the curve Π(t) on the sphere and is oriented according to the right-hand rule, and k is an integer (reflecting the fact that we are really only interested in angles up to multiples of 2π).

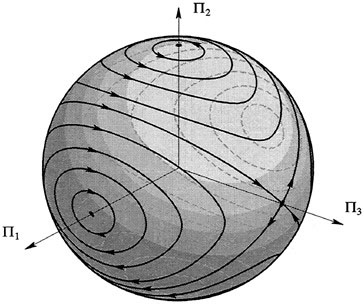
FIGURE 1.5 The solutions of Euler's equations for rigid body motion.

An interesting feature of this formula is the fact that Δθ splits into two parts. The term A is the purely geometric quantity, the geometric phase. It does not depend on the energy of the system or the period of motion, but rather on the fraction of the surface area of the sphere that is enclosed by the trajectory. The second term, the dynamic phase, depends on the system's energy and the period of the trajectory.

Geometrically we can picture the rigid body as tracing out a path in its phase space; that is, the space of rotations (playing the role of positions) and corresponding momenta with the constraint of a fixed value of the spatial angular momentum. The phase space plays the role of the bundle, and the projection map to the base, the momentum sphere, is the map we described earlier that takes the orientation A and its velocity (or momentum) to the body momentum sphere. As Figure 1.5 shows, almost every trajectory on the momentum sphere is periodic, but this does not imply that the original curve of rotations was periodic, as is shown in Figure 1.6. The difference between the true trajectory and

a periodic trajectory is given by the geometric plus the dynamic phase. Although this figure is given in the context of rigid body dynamics, its essential features are true for any mechanical system with symmetry.

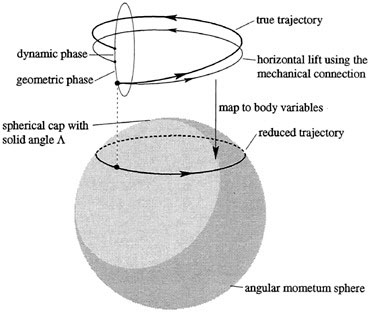
FIGURE 1.6 The geometric phase formula for rigid body motion.

This formula for the rigid body phase has a long and interesting history. It was known in classical books, such as that of Whittaker, in terms of quotients of theta functions, but not in terms of areas, as above. This aspect was discovered in the 1950s independently in work of Ishlinskii and of Goodman and Robinson. Montgomery (1991b,c) and Marsden et al. (1990) showed, following the lead of Berry and Hannay, that the formula can be interpreted in terms of holonomy of a connection. Further historical details may be found in Marsden and Ratiu (1994).

It is possible to observe some aspects of the geometric phase formula for a rigid body with a simple experiment. Put a rubber band around a book so that the cover will not open. (A tall thin book works best.) With the front cover facing up, gently toss the book in the air so that it rotates about its middle axis. Catch the book after a single rotation and you will find that it has also rotated by 180º about its long axis; that is, the front cover is now facing the floor.

In addition to its use in understanding phases, the mechanical connection has been helpful in stability theory. For example, when a rigid body such as a satellite tumbles about its long or short axis, it does so stably, but it is unstable when it rotates about the middle axis. When one takes into account small dissipative effects such as a vibrating antenna, then the rotational motion about the long axis becomes 

unstable as well, but this effect is more delicate. Corresponding statements for systems like rigid bodies with flexible appendages or interconnected rigid bodies are more subtle than the dynamics of a single rigid body. There is a powerful method for determining the stability of such solutions called theenergy momentum method. This method is an outgrowth of basic work of Riemann, Poincaré, and others in the last century and more recently by Arnold; further recent developments were made by Simo et al. (1991), and Bloch et al. (1994, 1996) and references therein. Here the main problem is to split the variables properly into those that correspond to internal, or shape, changes, and to those that correspond to rotational and translational motions. Interestingly, the mechanical connection plays a key role in the solution of this problem and it makes many otherwise intractable problems soluble.

This gauge theory of mechanics has been successful for a number of important problems, such as the falling cat problem, as we shall discuss below. Nevertheless, there is another important class of problems that it does not apply to as stated, namely, mechanical systems with rolling constraints, typified by the constraint that a wheel or ball rolls without slipping on a plane. One very simple idea ties this type of problem to the zero angular momentum constraint problem that was just described. This idea is that of realizing the constraint as the horizontal space of a connection. In fact, the constraint itself defines a connection by declaring the constraint space to be the horizontal space. This, in effect, defines the connection. In the case of rolling constraints, we call this connection the kinematic connection to avoid confusion with the mechanical connection described earlier. This point of view for systems with rolling (and rolling type) constraints was developed by Koiller (1992) and by Bloch et al. (1997). For example, the equations of motion expressed on the base space again involve the curvature of the kinematic connection. This shows again that the links with geometry are strong at a very basic level.

Things get even more interesting when the system has both rolling constraints and symmetry. Then we have the kinematic connection as well as the symmetry group to deal with, but now they are interlinked. One of the things that makes systems with rolling constraints with symmetry different from free systems is that the law of conservation of angular momentum is no longer valid for them. This is already well illustrated by a toy called the rattleback, a canoe-shaped piece of wood or plastic. When the rattleback rocks on a flat surface like a table, the rocking motion induces a rotational motion, so that it can go from zero to nonzero angular momentum about the vertical axis as a result of the interaction of the rocking and rotational motion and the rolling constraint with the table. One can say that the forces of constraint that enforce the condition of rolling can upset the balance of angular momentum. This is also the case for the snakeboard discussed below, but nonetheless, this rams out to be a key point in understanding locomotion generation for this system. One of the interesting aspects of this is that, as shown by Bloch et al. (1996), there is a very nice equation satisfied by a particular combination of the linear and angular momentum, which they call the momentum equation. Because of that success, one can imagine that this understanding will be important for many other similar systems as well.