STABILIZATION AND OPTIMAL CONTROL

Control theory is closely tied to dynamical systems theory in the following way. Dynamical systems theory deals with the time evolution of systems by writing the state of the system, say z in a general space P, and writing an evolution equation

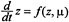
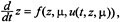
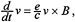
for the motion, where μ includes other parameters of the system (masses, lengths of pendula, etc.). The equations themselves include things like Newton's second law, the Hodgkin-Huxley equations for the propagation of nerve impulses, and Maxwell's equations for electrodynamics, among others. Many valuable concepts have developed around this idea, such as stability, instability, and chaotic solutions.

Control theory adds to this the idea that in many instances, one can directly intervene in the dynamics rather than passively watching it. For example, while Newton's equations govern the dynamics of a satellite, we can intervene in these dynamics by controlling the onboard gyroscopes. One simple way to describe this mathematically is by making f dependent on additional control variables u that can be functions of t, z, and μ. Now the equation becomes

and the objective, naively stated, is with an appropriate dependence of f on uto choose the function u itself to achieve certain desired goals. Control engineers are frequently tempted to overwhelm the intrinsic dynamics of a system with the control. However, in many circumstances (fluid control is an example—see, for example, the discussion in Bloch and Marsden, 1989), one needs to work with the intrinsic dynamics and make use of its structure.

Two of the basic notions in control theory involve steering and stabilizability. Steering has, as its objective, the production of a control that has the effect of joining two points by means of a solution. One imagines manipulating the control, much the way one imagines driving a car so that the desired destination is attained. This type of question has been the subject of extensive study and many important and basic questions have been solved. For example, two of the main themes that have developed are, first, the Lie algebraic techniques based on brackets of vector fields (in driving a car, you can repeatedly make two alternating steering motions to produce a motion in a third direction) and, second, the application of differential systems (a subject invented by Elie Cartan in the mid-1920s whose power is only now being significantly tapped in control theory). The work of Tilbury et al. (1993) and Walsh and Bushnell (1993) typify some of the recent applications of these ideas.

The problem of stabilizability has also received much attention. Here the goal is to take a dynamic motion that might be unstable if left to itself but that can be made stable through intervention. A famous example is the F-15 fighter, which can fly in an unstable (forward wing swept) mode but which is stabilized through delicate control. Flying in this mode has the advantage that one can execute tight turns with rather little effort—just appropriately remove the controls! The situation is really not much different from what people do everyday when they ride a bicycle. One of the interesting things is that the subjects that have come before—namely, the use of connections in stability theory—an be turned around to be used to find useful stabilizing controls, for example, how to control the onboard gyroscopes in a spacecraft to stabilize the otherwise unstable motion about the middle axis of a rigid body (see Bloch et al., 1992; Kammer and Gray, 1993).

Another issue of importance in control theory is that of optimal control. Here one has a cost function (think of how much you have to pay to have a motion occur in a certain way). The question is

not just if one can achieve a given motion but how to achieve it with the least cost. There are many well-developed tools to attack this question, the best known of these being what is called the Pontryagin Maximum Principle. In the context of problems like the falling cat, a remarkable consequence of the Maximum Principle is that, relative to an appropriate cost function, the optimal trajectory in the base space is a trajectory of a Yang-Mills particle. The equations for a Yang-Mills particle are a generalization of the classical Lorentz equations for a particle with charge e in a magnetic field B:

where v is the velocity of the particle and where c is the velocity of light. The mechanical connection comes into play though the general formula for the curvature of a connection; this formula is a generalization of the formula 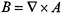 expressing the magnetic field as the curl of the magnetic potential. This remarkable link between optimal control and the motion of a Yang-Mills particle is due to Montgomery (1990, 1991a).

One would like to make use of results like this for systems with rolling constraints as well. For example, one can (probably naively, but hopefully constructively) ask what is the precise connection between the techniques of steering by sinusoids mentioned earlier and the fact that a particle in a constant magnetic field also moves by sinusoids, that is, moves in circles. Of course if one can understand this, it immediately suggests generalizations by using Montgomery's work. This is just one of many interesting theoretical things that requires more investigation. One of the positive things that has already been achieved by these ideas is the beginning of a deeper understanding of the links between mechanical systems with angular momentum type constraints and those with rolling constraints. The use of connections has been one of the valuable tools in this endeavor. One of the papers that has been developing this point of view is that of Bloch et al. (1997). We shall see some further glimpses into that point of view in the next section.