Understanding, Calculating, and Measuring Total Harmonic Distortion (THD)

Total harmonic distortion (THD) is a measurement that tells you how much of the distortion of a voltage or current is due to harmonics in the signal. THD is an important aspect in audio, communications, and power systems and should typically, but not always, be as low as possible.

Introduction

Harmonics or harmonic frequencies of a periodic voltage or current are frequency components in the signal that are at integer multiples of the frequency of the main signal. This is the basic outcome that Fourier analysis of a periodic signal shows. Harmonic distortion is the distortion of the signal due to these harmonics.

A voltage or current that is purely sinusoidal has no harmonic distortion because it is a signal consisting of a single frequency. A voltage or current that is periodic but not purely sinusoidal will have higher frequency components in it contributing to the harmonic distortion of the signal. In general, the less that a periodic signal looks like a sine wave, the stronger the harmonic components are and the more harmonic distortion it will have.

So, a purely sinusoidal signal has no distortion while a square wave, which is periodic but does not look sinusoidal at all, will have lots of harmonic distortion. In the real world, of course, sinusoidal voltages and currents are not perfectly sinusoidal; some amount of harmonic distortion will be present. Figures 1 and 2 provide visual comparisons, in the time domain and the frequency domain, of a sinusoidal voltage and a square wave voltage.

Figure 1. A sinusoidal voltage and a square wave voltage in the time domain.

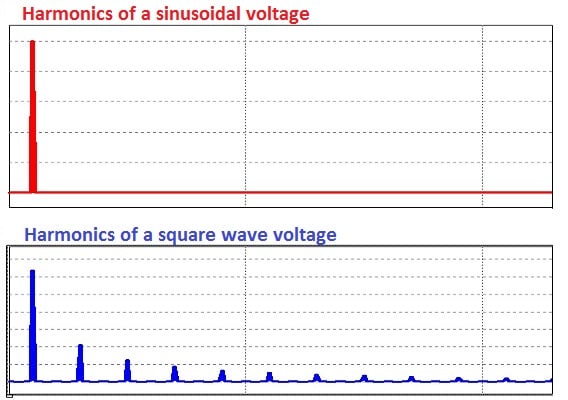
Figure 2. A sinusoidal voltage and a square wave voltage in the frequency domain; only the square wave has peaks at the harmonic frequencies.

It is easy to see the harmonic distortion when examining the time domain and frequency domain representations of a square wave, but it is also important to be able to quantify harmonic distortion. The next section shows how to do that with the metric of total harmonic distortion.

Calculating Total Harmonic Distortion

THD is defined as the ratio of the equivalent root mean square (RMS) voltage of all the harmonic frequencies (from the 2nd harmonic on) over the RMS voltage of the fundamental frequency (the fundamental frequency is the main frequency of the signal, i.e., the frequency that you would identify if examining the signal with an oscilloscope). Equation 1 shows the mathematical definition of THD (note that voltage is used in this equation, but current could be used instead):

THD=∑∞n=2V2n_rms−−−−−−−−−−√Vfund_rms

      Equation 1

• Vn_rms

is the RMS voltage of the nth harmonic

Vfund_rms

•  is the RMS voltage of the fundamental frequency

Since the amplitudes of the harmonics are needed to calculate the THD, Fourier analysis can be used to help determine THD. To see this application of Fourier analysis, let’s look at the simple example of a 50% duty cycle square wave. The Fourier series representation of a 50% duty cycle square wave is the following:

vsquare(t)=4π∑n=1,3,5...∞sin(2nπft)n

      Equation 2

And in expanded form, this is:

vsquare(t)=4πsin(2πft)+43πsin(6πft)+45πsin(10πft)+...+4nπsin(2nπft)

      Equation 3

The expanded form is useful to look at because it highlights the peak voltage (V_pk) of each frequency component, and the THD can be calculated by determining the RMS value (i.e.,

Vpk2–√

) of each frequency component and plugging them all in to Equation 1:

THDsquare=(432√π)2+(452√π)2+(472√π)2+...+(4n2√π)2−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−√42√π

       Equation 4

This equation is starting to get unwieldy, but one thing to notice is that every term in the expression has a

42–√π

component. This component can be factored out, and since it appears in both the numerator and denominator, it actually cancels out, which leaves the expression for THD of a square wave as follows:

THDsquare=∑∞n=3,5,...1n2−−−−−−−−−√1=132+152+172+...+1(n)2−−−−−−−−−−−−−−−−−−−−−√

       Equation 5

To calculate the THD from this expression requires a tricky little bit of mathematics. If the summation under the square root in Equation 5 started at n=1, then it would be a convergent series that adds up to

π28

:

∑n=1,3,5...∞1n2=π28

       Equation 6

The only difference between the expression in Equation 6 and the one in the THD calculation of Equation 5

(∑n=3,5,...∞1n2)

is the value of

1n2

when n is 1. Since this value is 1, the summation in the THD expression can be re-written as:

∑n=3,5,...∞1n2=∑n=1,3,5...∞1n2−1=π28−1

       Equation 7

Finally, plugging this equation back into the THD equation for the square wave (Equation 5) gives:

THDsquare=π28−1−−−−−−√≈0.483

       Equation 8

Our assumption at the beginning that a square wave has a lot of harmonic distortion was based on visually examining the square wave in the time and the frequency domain. The calculations that we just went through confirm our assumption. A square wave actually has about 48.3% total harmonic distortion meaning that the RMS of the harmonics is about 48.3% of the RMS of the fundamental frequency.

Measuring Total Harmonic Distortion

Calculating theoretical THD can be a good exercise, but it can be a lot of work, and in practice, you aren’t going to get an ideal signal (e.g., a perfect square wave) anyway. The outcome of these calculations can therefore only give an approximation for the THD that you might get for a given signal type. In practice, THD must be measured to obtain the RMS value of the fundamental frequency and all of the harmonics. This measurement can be done in a couple of ways.
In the first method, filters can be used to split the signal into two parts: a signal with all of the harmonics filtered out leaving just the fundamental frequency, and a signal with the fundamental frequency filtered out leaving all of the harmonics. Then the RMS value of each of those two parts can be measured and the THD calculated:

THD=VRMS_Without_FundamentalVRMS_Fundamental

The upside of this method is that it is easy to perform these measurements. The downside is that noise will also be included in the measurement so you actually get a measurement of THD plus noise (although in audio systems THD+noise is actually an important measurement too).
The second method for measuring THD is to measure the amplitude of the fundamental frequency and each harmonic and then use those measurements to calculate THD using Equation 1. This measurement can easily be done using a spectrum analyzer or a THD analyzer which will execute Equation 1 automatically. An alternative measurement technique is to capture voltage or current data and then perform a Fourier transform on the data collected. The example below outlines how this second method is used.

Example THD Measurement

The example block diagram in figure 3 shows a 1 kHz sine wave passing through an amplifier to create a new 1kHz sine wave that has some crossover distortion. This new wave is fed in to a spectrum analyzer which gives a graphical display of the amplitude of a number of the harmonics.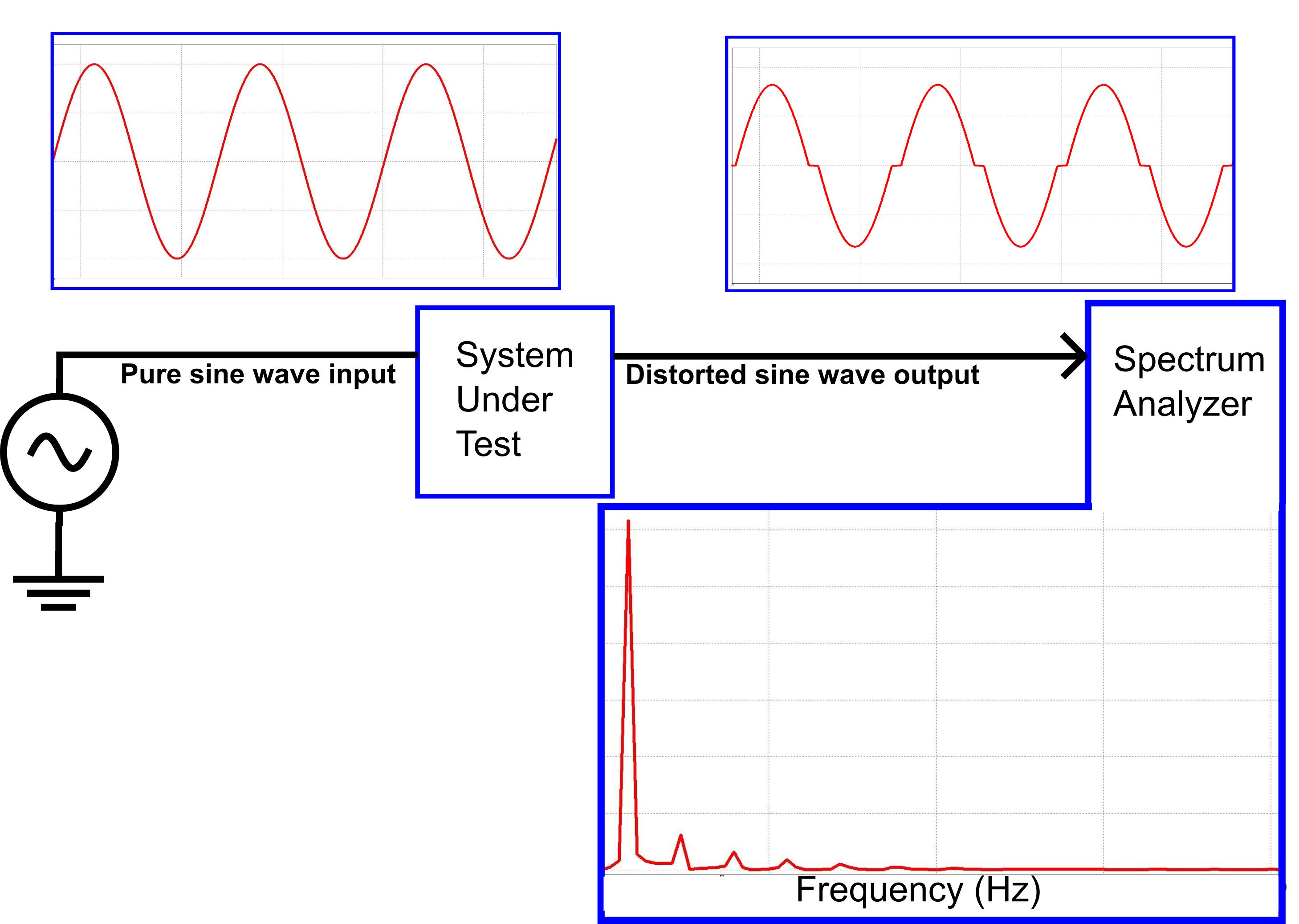

Figure 3. A system that introduces crossover distortion into a signal.

Zooming in on the frequency spectrum of the distorted sine wave output, we can see the amplitudes at several of the harmonic frequencies:

Figure 4. Frequency spectrum of sinusoidal voltage with crossover distortion.

From this frequency spectrum, I manually measured the amplitude of each of the harmonic frequencies and recorded the data in the table below:

Amplitudes of Harmonics of Distorted Sine Wave

Harmonic	Amplitude
1	3.08V
3	0.308V
5	0.159V
7	0.090V
9	0.0487V
11	0.0253V
13	0.0164V
15	0.010V

The amplitudes of even-numbered harmonics and harmonics above the 15th are nearly 0, so I didn’t include them in my calculation.
The measured amplitudes are plugged in to the THD equation:

THD=0.3082+0.1592+0.0902+0.04872+0.02532+0.01642+0.0102−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−√3.08

(note that I am able to use the voltage amplitudes instead of RMS voltage because

VRMS=Vp2–√

and since the

2–√

occurs in all terms, it can be factored out and cancelled).
This calculation gives a THD of 0.118 or 11.8%.
Of course a THD analyzer would automate the process of calculating THD from the amplitudes of the harmonics. Using a THD analyzer for this signal gives a value of 11.9%, which confirms the accuracy of the manual method that I just went through.

Final Words

This article has provided some background about THD and how to determine it, both theoretically and in a real (simulated) system. But it has not discussed the kinds of systems where THD is an important measurement.

THD is important in several types of systems, including power systems, where a low THD means higher power factor, lower peak currents, and higher efficiency; audio systems, where low THD means that the audio signal is a more faithful reproduction of the original recording; and communication systems, where low THD means less interference with other devices and higher transmit power for the signal of interest.

Look for future articles where I will go into more detail about these specific types of systems.